GAMES203-02 Registeration 配准
GAMES203-02 Registeration 配准
What is Registeration?
Registeration refers to align two shapes/scans (such as point clouds) give an intial guess for relative transform.
This paragraph includes a sidenoteWhen the initial pose is rough, robust correspondence filtering often improves convergence before full ICP refinement. to emphasize the practical setup insight.
You can also add a margin noteIn this post layout, margin notes stay in the outer column on desktop and collapse into a toggle block on smaller screens..
Classifications of the task
Fully Overlap vs Partially Overlap
Fully Overlap: one point cloud could be anothers copy or be included. e.g. error measurement between products and prototype.
Partially Overlap: Each point cloud has only some part overlap with the others. e.g. 3d scans from different aspects.
Global vs Local:
Global: Poses generating the original point clouds are quite different.
Local: Poses are generally close. So point clouds are basically aligned.
Pairwise vs Multiple:
Pairwise: align two point clouds.
Multiple: align multiple point clouds. (Which we need for 3d reconstruction.)
Pairwise registeration
Fully overlap
If we already know correct point correspondences, we could easily construct a error function from them. (suppose no non-rigid transformation, only rotation/translation)
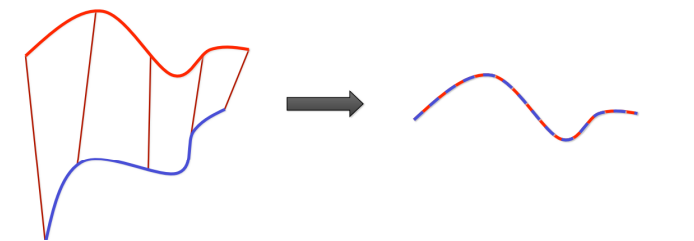
E := ∑i(Rpi + t − qi)2
And the equation has a closed form solution.
ICP(Iterative Closest Point) Algorithm
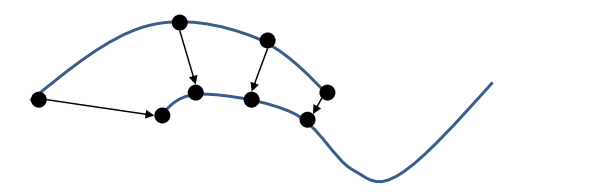
But since we have no known correspondence for real data, if two point clouds has close enough starting poses, for point in one point cloud we just assume that the closest point (nearest neighbor) in another point cloud as its corresponding point.
In each iteration, we sample some points from one point cloud and find their nearest neighbors. Then according to the correspondence, we could solve it again using the method above. If starting poses are close enough, iteration will converge.
The nearest neighbor pairs could be easily obtained with packages or using kd trees/ squared distance field.
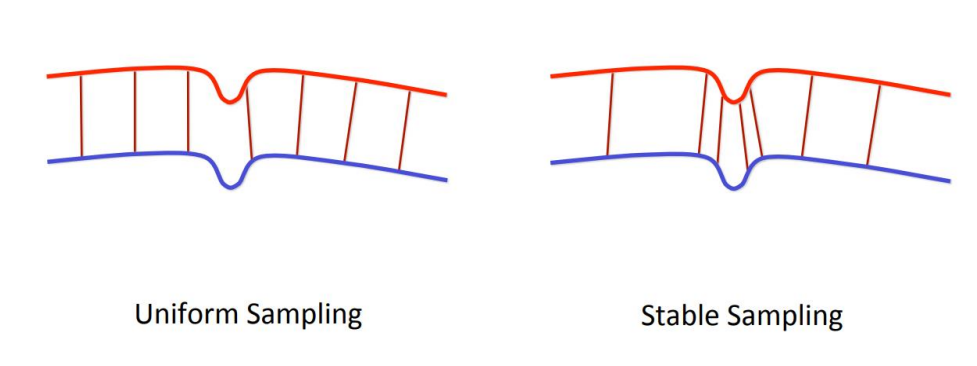
Sampling strategies also matter. Stable sampling could better constraint the degrees of freedom than uniform sampling. See Geometrically Stable Sampling for the ICP Algorithm, Gelfand et al.
From the optimization perspective
The problem we are optimizing could be formulated as a least squares:
F(α) = ∑id2(α(xi0), Φ)
where α is a rigid body transformation.
Plain ICP
linear convergence
suppose point-to-point correspondence
usually solve directly with SVD (formula see 三维点云配准)
depend on the initial guess: need a closer initial value.
Limitation helps: anchor points using feature matching, add assumptions to limit the degree of freedom.
Variants of ICP: Point-to-Plane ICP, Plane-to-Plane ICP, GICP, NICP
employ more complex error functions.
less sensitive to initial guess, avoid local minima.
since distance is not just plain residual, it is turned into a non-linear least sqaure problem.
Often solve with Gauss-Newton method, which use first-order linearity to approximate the nonlinearity:
Δ = −(JrTJr)−1JrTr(β(s))
whereβ is the variable,${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{m}r_{i}({\boldsymbol {\beta }})^{2}}$, ${\displaystyle \left(\mathbf {J_{r}} \right)_{ij}={\frac {\partial r_{i}\left({\boldsymbol {\beta }}^{(s)}\right)}{\partial \beta _{j}}}}$.
Plane-to-Plane: See Object modeling by registeration of multiple range images and Geometry of the Squared Distance Function to Curves and Surfaces
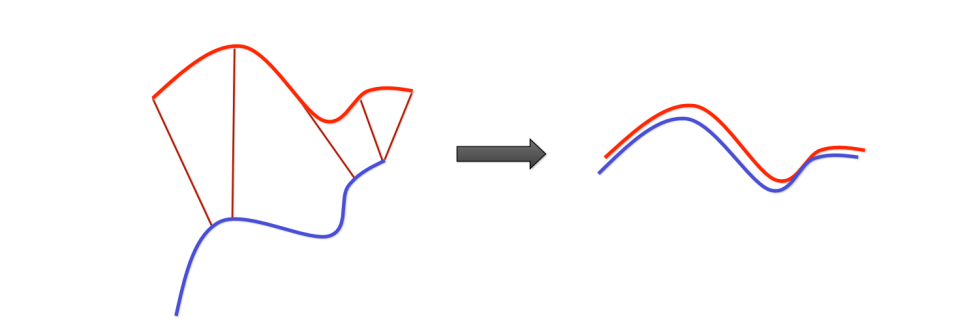
Partial overlap
If only a part of the point cloud is overlapped, we usally deal with:
Use robust functions/robust norm instead of L2 norm under point-2-plane distance metric.
like $\rho_{GM} = \frac{t^2}{\sigma^2+t^2}$ or L1 norm. Optimize still with Gauss-Newton.
A robust norm as its name, is more robust to those irregular data.
IRLS(Iterationally Reweighted Least Square) for p-norm
Problem: optimize objective function $\arg\min_\beta \sum_{i=1}^n|y_i-f_i(\beta)|^p$
transform and thus introduce weight into least square
$$ \arg \min_\beta \sum_{i=1}^n w_i |y_i-x_i\beta|^2 $$
where in particular wi is updated in each iteration with wi = |yi − xiβ|p − 2
In this way, we solve a reweighted optimize problem in each iteration. Often with a well-chosen weight function(in this case the L1 or Lp norm), those outliers will has lower weight and thus influence of unmatched part will be reduced.(general case see M-estimator IRLS)
Optimize with closed form solution(linear case) or Gauss-Newton/Levenberg-Marquardt(for nonlinear case)
Bi-directional pruning
For r1 in M, find its nearest neighbor q1 in P, and find q1’s nearest neighbor v1 in M, in those unmatched case r1 and v1 are distant. thus in this way we can filter out those unmatched outliers.
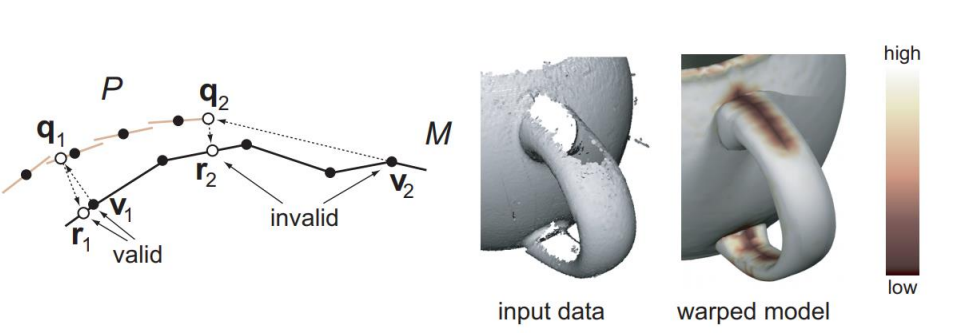
Variants of ICP see Efficient variants of ICP
