Perron-Frobenius定理及其应用

概述

特征值和特征向量理论提供了简化矩阵运算和理解刻画矩阵性质的工具,其中Jordan标准型理论给出了复数矩阵的一种最简形式,是刻画矩阵性质、进行计算的一种简便方法. 但在许多实际问题中由于矩阵规模大、Jordan标准型求解方法的数值稳定性差等原因难以使用Jordan标准型进行数值计算.故而我们需要应用Gershgorin圆盘定理等来获得矩阵的特征值这一重要信息.

特别的,对于正矩阵（非负矩阵）,我们有Perron定理（Perron-Frobenius定理）,由于正矩阵（非负矩阵）这类特殊矩阵在现实数据中的普遍出现,这一定理在概率论、统计学乃至经济学、搜索引擎排名中都得到了广泛应用.

正矩阵的Perron定理

证明中涉及的\(>\)等关系均定义为按照元素比较(所有元素均大于),含义是显然的.

对于正矩阵,我们有如下的Perron定理：

定理 1. 设\(A\)是一正方阵. 则有

1. \(A\)的谱半径\(\rho(A)=\max\{|\lambda_i|\}\)是\(A\)的一个单特征值
2. \(A\)有一个属于\(\rho(A)\)的正特征向量
3. \(A\)的其余特征值\(\lambda\)均无非负特征向量 此时矩阵\(A\)的谱半径\(\rho(A)\)被称作\(A\)的Perron根,属于Perron根的正特征向量称为\(A\)的Perron向量.

对于这一定理最为简洁的一种证明方法是由G. Debreu和I. N.Herstein提出的利用Brouwer不动点定理的证明.现给出一个同样利用Brouwer不动点定理的证明：

引理 2. (Frobenius)\(A\)有一正特征值,且该特征值有正的特征向量

Proof. 设\(S\)是\(R^n\)中单位球上(其上的点记为\((x_1,\cdots,x_n)\))所有满足\(|x_i|\geq 0,\forall i\in\{1,\cdots,n\}\)构成的子集. 定义一个映射\(T\),\(T(v)=Av/|Av|\),由于\(A\)中各元素为正数,对\(\forall v\in S\),必然有\(Av>0\)（因\(v\)中各分量不全为0,与全正的行向量点积结果必然为正）,从而有\(||Av||>0\),\(Av/||Av||\in S\),从而\(T\)是从S到其自身的连续映射. 且由于S同胚于\(n-1\)维闭单位球,由Brouwer不动点定理知\(\exists v_0,s.t. Av_0=||Av_0||v_0\),此时\(v_0\)便是\(A\)的特征向量,特征值为\(||Av_0||\),由上述证明知这组特征向量和特征值均为正. ◻

下设引理2.2中的这组特征值-特征向量对为(r,v)

引理 3. \(r\)没有其他与\(v\)线性无关的特征向量（即\(r\)对应的几何重数为1,\(A\)的Jordan标准型中\(r\)仅对应一个Jordan块）

Proof. 反证法.若\(r\)有另一与\(v\)线性无关的特征向量\(x\),不妨假定它是实向量且也是正的（若非正,可加上\(v\)的若干倍使其变为正的而不影响线性相关性；复特征向量可通过取共轭方式发现实部和虚部向量均为\(r\)的特征向量,从而\(r\)的特征向量空间必有实向量组成的基,从而只需要研究实向量）. 由于\(v\),\(x\)是同特征值对应的特征向量,令\(t=\min\{\frac{v_i}{x_i}|x_i>0\}\),则\(y=v-tx\)必定有一分量为0,且\(y\)仍为\(r\)的特征向量.但是根据引理2.2的证明,非负的特征向量必然是正的,从而产生了矛盾. ◻

引理 4. \(r\)是一个单特征值

Proof. 我们已经知道,\(r\)对应的Jordan块只有一个.现要证这一Jordan块必然是1*1的. 不妨假设\(r=1\),或令\(A'=A/r\)从而有\(r=1\).从而对于对应的正特征向量\(v\)我们有:\(||v||_\infty =||A^kv||_\infty\min_i(v_i)\),从而\(||A^k||_\infty\leq||v||/min_i(v_i)\),\(||A^k||_\infty\)必然是有界的
然而另一方面,如果Jordan块大小不为1,则考虑Jordan块的左上2*2部分\(J'\),\(J'^k=\left(\begin{array}{cc} \lambda & 1\\ 0 &\lambda \end{array}\right)^k=\left(\begin{array}{cc} \lambda^k & k\lambda^{k-1} \\0 &\lambda^k \end{array}\right)\),从而\(||J'^k||_\infty=|k+\lambda|=|k+1|\),必然无界,又由Jordan标准型的形式知\(J'^k\)必然是\(J^k\)的一个子矩阵且在\(J^k\)中对应\(J'^k\)的两列的列和仍与\(J'^k\)两列的列和相等.从而必有\(||J^k||_\infty\geq||J'^k||_\infty\)无界 又\(J^k=C^{-1}AC\),故由矩阵范数的性质知\(||J^k||= ||C^{-1}AC||\leq||C^{-1}||||A^k||||C||\),从而由\(||J^k||\)无界推知\(||A^k||\)必然无界.产生矛盾,故\(r\)的代数重数只能为1 ◻

事实上,上述证明也适用于其他正的特征值-特征向量对,所以我们已经证明了\(r\)能够与\(v\)所在特征向量系一一对应

引理 5. \(A\)的其余特征值\(\lambda\)均没有正特征向量（即\(v\)是\(A\)的唯一正特征向量（作为基的意义下））

Proof. 反证法.若我们有\(r_1\),\(r_2\)(\(r_1\not=r_2\))两个具有正特征向量的特征值,不失一般性地设\(r_1<r_2\). 两特征值对应的特征向量\(v\),\(x\)线性无关,同样设\(t=\min\{\frac{v_i}{x_i}\}=\frac{v_m}{x_m}\),\(y=v-tx\),则同理\(y\)非负非零且必有一分量为0,从而\(Ay=r_1v-r_2tx\)是一正向量,故\(r_1v_m-r_2tx_m>0\). 但是\(r_1v_m=r_2tx_m\leq r_2 tx_m\),矛盾. ◻

到这里我们已经证明了正特征值-特征向量对\((r,v)\)是唯一的.从而接下来只需要证明\(r\)对应A的谱半径\(\rho(A)\).

不加证明地给出如下公式：

定理 6. (Gelfand) 对任意矩阵范数有\(\rho(A)=\lim_{k\rightarrow \infty}||A^k||^{\frac{1}{k}}\).

推论 7. \(A,B\)均为正矩阵,如果\(A\geq B\),则\(\rho(A)\geq\rho(B)\)

Proof. 对\(\forall m\in\mathbb{N}_+\),由\(A\geq B\)能够自然推知\(A^m\geq B^m\),考虑矩阵的1-范数,由\(A^m\)中各列和对应的大于等于\(B^m\)中的各列和,从而有\(||B^m||_1\leq A^m\)中的各列和,进而\(||A^m||_1^{1/m}\geq||B^m||_1^{1/m}\),此时令\(m\rightarrow \infty\),便有\(\rho(A)\geq\rho(B)\) ◻

引理 8. \(\min_{1\leq i\leq n} x_i^{-1}\sum_{j=1}^n a_{ij}x_j\leq\rho(A)\leq \max_{1\leq i\leq n} x_i^{-1}\sum_{j=1}^n a_{ij}x_j\),\(x_i>0\)

Proof. 由Gerschgorin圆盘定理知,\(\exists i,|\rho(A)-a_{ii}|\leq\sum_{j=1,j\not=i}^n |a_{ij}|\),从而有\(\exists i,|\rho(A)|-|a_{ii}|\leq|\rho(A)-a_{ii}|\leq\sum_{j=1,j\not=i}^n |a_{ij}|\),从而\(\rho(A)\leq \max_{1\leq i\leq n}\sum_{j=1}^n|a_{ij}|\) .设\(a=\min_{1\leq i\leq n} \sum_{j=1}^n a_{ij}\),通过在第i行上乘上\(\frac{a}{\sum_{j=1}^n a_{ij}}\)得到一个新矩阵\(B\)且\(B\leq A\),从而显然\(a\)是\(B\)的一个特征值,对应的特征向量为\([1,1,\cdots,1]^T\),进而结合推论2.7和谱半径的定义有\(a\leq \rho(B)\leq\rho(A)\).

从而我们得到\(\min_{1\leq i\leq n} \sum_{j=1}^n a_{ij}\leq \rho(A)\leq\max_{1\leq i\leq n} \sum_{j=1}^n a_{ij}\) 考虑矩阵\(S=diag(x_1,x_2,\cdots,x_n)\),显然由\(x_i>0\)知\(S\)可逆,\(S^{-1}AS>0\),那么\(\rho(S^{-1}AS)=\rho(A)\),进而结合上式对谱半径的估计,直接导出\(\min_{1\leq i\leq n} x_i^{-1}\sum_{j=1}^n a_{ij}x_j\leq\rho(A)\leq \max_{1\leq i\leq n} x_i^{-1}\sum_{j=1}^n a_{ij}x_j\) ◻

定理 9. 若\(\lambda\)是\(A\)的特征值,\(|\lambda|=\rho(A)\),对应的特征向量为\(x\),则\(|\lambda|\)是\(A\)的一个特征值（即\(\rho(A)\)是\(A\)的特征值）,对应的特征向量为\(|x|\),\(|x|>0\)

Proof. \(\rho(A)x=|Ax|\leq |A||x|=A|x|\),从而\(y=A|x|-\rho(A)|x|\geq 0\).
\(y=0\)时,\(A|x|=\rho(A)|x|\)自然成立且由引理2.2\(\rho(A)>0\),故由引理2.2证明过程同样有\(|x|>0\),结论成立.
\(y>0\)时,不难推知\(Ay>0\),设\(z=A|x|\),写成\(Az>\rho(A)z\),进而\(\rho(A)<\min_{1\leq i\leq n}z_i^{-1}\sum_{j=1}^n a_{ij}z_j\),结合\(z\)必为正向量和引理2.8,该式不可能成立 从而得知\(y=0\),从而定理证毕 ◻

定理 10. 设\(A\)是一正方阵. 则有

1. \(A\)的谱半径\(\rho(A)=\max\{|\lambda_i|\}\)是\(A\)的一个单特征值
   

2. \(A\)有一个属于\(\rho(A)\)的正特征向量
   

3. \(A\)的其余特征值\(\lambda\)均无非负特征向量
   此时矩阵\(A\)的谱半径\(\rho(A)\)被称作\(A\)的Perron根,属于Perron根的正特征向量称为\(A\)的Perron向量.

   Proof. 由定理2.9,\(\rho(A)\)必然是A的一个特征值,且它对应一个正特征向量.根据引理2.2-2.5的证明,\(A\)具有唯一的一对正特征值-特征向量对,即为\(\rho (A)\)和对应的特征向量\(|x|\). 从而根据引理的结论,它是一单特征值,且其余的特征值\(\lambda\)均没有非负（在正矩阵条件下与正等价）的特征向量.定理证毕. ◻

非负矩阵的Perron-Frobenius定理

对于某些类型的非负矩阵,我们能够给出相似的结论:

定义 11. 如果存在置换矩阵P使得非负矩阵A有:\(P^\mathrm{T}AP=\left(\begin{array}{cc} B &C\\0&D \end{array}\right)\)其中B,C,D均为非负矩阵,则称非负矩阵\(A\)是可约的.否则称为不可约矩阵.

定理 12. 设\(A\)是一不可约非负方阵. 则有

1. \(A\)的谱半径\(\rho(A)=\max\{|\lambda_i|\}\)是\(A\)的一个单特征值
2. \(A\)有一个属于\(\rho(A)\)的正特征向量
3. \(A\)的其余特征值\(\lambda\)均无非负特征向量 此时矩阵\(A\)的谱半径\(\rho(A)\)被称作\(A\)的Perron根,属于Perron根的正特征向量称为\(A\)的Perron向量.

对于不可约非负方阵同样有利用Brouwer不动点定理或Banach不动点定理的证明, 亦有Wielandt利用Collatz-Wielandt函数进行的证明.由于笔者能力以及篇幅有限,不再对其做进一步证明.

Perron-Frobenius定理的应用:PageRank算法

互联网的有向图模型

PageRank这一算法目的在于计算互联网网页的重要度.我们希望能够在网页集合上定义一个函数\(PR\),它对每个网页给出对应的PageRank值,PR值越高就代表这一网页越重要.

假定互联网是一有向图,用有向图的结点代表网页,有向边代表网页之间随机跳转的概率.并且我们假定从一个网站链接出去的超链接都被等概率访问.

一个假想的互联网有向图

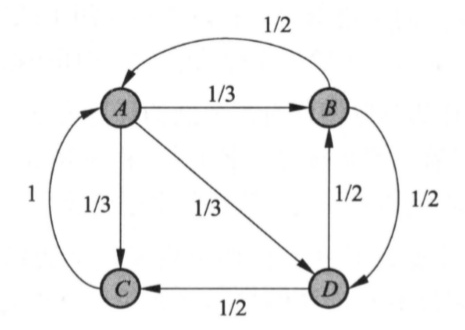
直观来看,指向一个网页的超链接越多\(\Leftrightarrow\)随机跳转到该网页的概率就越高\(\Leftrightarrow\)该网页的PageRank值就越高. 这也就促使我们考虑将极限情况下各个结点被访问到的概率作为其PageRank值,用于表示结点的重要度.

随机游走模型与PageRank的基本定义

在上述互联网的有向图模型上定义随机游走模型（一阶马尔可夫链）,结点表示状态,有向边表示状态之间的转移,一个节点到它通过有向边连接到的所有节点转移概率相等. 如果将概率作为边权,那么转移矩阵即为有向图的邻接矩阵\(M\). 其中\(M_{ij}=\begin{cases} \frac{1}{k} & \text{存在从j到i的有向边} \\ 0 & \text{others.} \end{cases}\)(从j出发的有向边共k条).不难发现\(M\)是非负矩阵,且各列和均为1. 由此我们考虑一个较为简单的情况,作为PageRank的基本定义:

若有向图为强连通（从任意结点出发可到任意结点）且非周期的，则称此时马尔科夫链的平稳分布\(R\)为这个有向图的PageRank,\(MR=R\). （\(R=[PR(v_1),PR(v_2),\cdots,PR(v_n)]\),\(PR(v_i)\)即为结点\(v_i\)的PageRank值）

根据马尔可夫链平稳分布定理,上述马尔可夫链在时间趋于无穷时状态分布收敛于唯一的平稳分布.

PageRank的一般定义与幂迭代法

上述PageRank的基本定义只能运用于强连通非周期情形,对于不连通的网络我们需要更强的定义：

我们可以进一步的考虑上网者除了从一个网站上的超链接跳到另一个网站的之外的行为——从一个网站随机的跳到所有网站中的任意一个 从而我们有基本定义中的基本转移矩阵\(M\)和一完全随机的转移矩阵\(M'\)，后者表示从任意结点到任意结点的转移概率均为1/n. 从而我们能够给出更一般的PageRank定义:满足\(R=d*MR+\frac{1-d}{n}*\bar{1}\),其中\(0\leq d\leq 1\)是预先给定的阻尼因子(表示上网者以d的概率按超链接随机跳转，或以1-d的概率进行完全随机跳转),\(\bar{1}\)表示所有分量为1的n维向量.

此处便是Perron-Frobenius定理发挥作用的地方.设\(E\)是一元素全为1的\(n\)阶方阵,进而从定义不难发现\(ER=\bar{1}\) 故PageRank一般定义式可以写作:\(R=(d*M+\frac{1-d}{n}*E)R=AR\)
可以发现A是一个正矩阵，那么根据我们已经证明的正矩阵的Perron-Frobenius定理(的一个略强的版本:正矩阵的谱半径是它的占优特征值),Pagerank向量R(一般定义下)是一般转移矩阵A的主特征向量,主特征值为1. 从而从一个初始的正向量开始,通过反复与A相乘,向量能够逐渐收敛到A的这一主特征向量.也就能够完成计算PageRank的过程.